[latexpage]

We all learn not to double dip. Not our nachos and not our models. So we split our dataset to 3: Training, Validation, and Test. We train on the Training set, optimize our parameters on the validation set, but to learn the real hard truth about our model generalization error we use the test set. But the story is off and disconnected to the way data scientists work. We don’t test a single model, we test many types of feature engineering techniques; we select features; and we test different types of classifiers, each one with its own set of hyper-parameters. Worse, most of the time we test these combinations sequentially, for instance, we compare a few types of classifiers, choose the one that performed best on our validation set and then try to improve our feature engineering. But sequential testing is essentially double-dipping, if we use our holdout set to choose a classifier, then it’s now contaminated and it cannot be used for anything else.

The problem of overfitting to the holdout set is evident in machine learning competitions, like the Zillow Prize, which we recently announced ( Round One recently closed). During these competitions, teams’ models are continuously evaluated against a common test set with undisclosed labels and their score is published on a public leaderboard. This creates a problem when teams start to incorporate feedback from the leaderboard into their model and overfit it to the test set, which improves their rank on the board, but reduces the model’s ability to generalize. Therefore, it is common to select a winner in these competitions by comparing the models on a second test set, which does not have a leaderboard (an example of someone that learned this the hard way).

For a real-world project, this is a very expensive solution. Creating multiple holdout sets in many scenarios can be time-consuming, and most of the time, we don’t know how many holdout sets we would need for our project.

In 2015, Dwork et al. published an elegant solution to this problem. Their work ties together concepts from two seemingly unrelated fields: statistical learning and differential privacy. Differential privacy is a field in cryptography that deals with the question of how to answer statistical queries regarding a dataset without exposing individual records. For instance, how can I provide access to a database of medical records but guarantee that the records won’t be traced to individuals? In this scenario, we are talking about statistical queries, for instance, to compute the average value of some column. The solution to such a problem is to provide access only through a mechanism that introduced controlled noise into the result. If we generate the noise in a smart way, we can prevent users from learning about individual records, but allow them to get results that are very close to what they would have got without any noise. An algorithm that accomplishes that is considered to be stable. In other words, if we can change one point in our dataset and the query result doesn’t change much then our algorithm is stable.

On the other side, we have the field of statistical learning, where we look for a model which can generalize well. But what does generalize mean? It means that it doesn’t overfit to a specific dataset, and produces similar results on similar datasets. Or in other words, our model generalizes well if we can change one point in our dataset and the model predictions do not change much. But this is exactly the definition we had for stability!! So a model that generalizes well is a stable model.

Dwork et al. showed that those two concepts are mathematically related, and therefore we can use algorithms developed for differential privacy to make sure our models will generalize. In the naive approach, which we practice every day, every time we evaluate our model we are basically “querying” the holdout set naively, exposing “individual records” and overfitting them. But if we will “query” the holdout set only through a stable algorithm, then we won’t see the noise of the “individual records”, and our algorithm will stay stable. This means that we will be able to use a single holdout set to all our evaluation needs from feature selection through parameter tuning to testing!!!

The algorithm itself, which is called Thresholdout is surprisingly simple. To formalize it we will denote our training set by S_t, our holdout set by S_h,  and a metric would like to compute (like accuracy) by M. In order to evaluate the model on the holdout set, we simply compute the absolute difference between the metrics of the two datasets: abs(M(S_t) – M(S_h)). If this difference is larger than a predetermined threshold $\tau$ we will return M(S_h) but with an additional small noise added. Otherwise, we will return the results of the training_set M(S_t).

Here is the pseudocode for the algorithm:

Given training set S_t, holdout set S_h and metric M, threshold $\tau$, and tolerance $\sigma$

\[
\break
$ $\xi \sim N(0, \sigma) \\
$\textbf{if} $ |M(S_t) - M(S_h)| > \tau + \xi \\
\indent \delta \sim N(0, \sigma) \\
\indent $\textbf{return} $ M(S_h) + \delta \\
$\textbf{else} $ \\
\indent $\textbf{return} $ M(S_t)
\]

*This version of Thresholdout was used in Dwork et al. paper, but the complete model that comes with all the mathematical guarantees has a few more lines, and use Laplacian noise. The full algorithm is in Fig S1. in here.

Does this seem too good to be true? Well, so is  but we don’t argue with math.

Before I give intuition to why this algorithm works, let’s see it in practice. For this I’ll use a simulation similar to the one used in the original paper (the full code): We are faced with a task of building a classifier on a small dataset consisting of 4000 rows and 2000 features. We split the dataset into a training set and a holdout set. To increase accuracy we decide to add a feature selection step, in which we select features in the training set which are correlated with the response variable. Since this step is prone to overfitting we need to validate that the selected features are also correlated with the response variable on the holdout set.

The correct way to do it is to have two separate holdout sets, one to validate the feature selection step and one to validate the classifier, but the idea here is to demonstrate how we can do this with a single holdout set. For control, we also calculated the classifier accuracy on a completely fresh dataset. The fresh dataset is made out of 10,000 to get an accurate estimate of the final classifier.

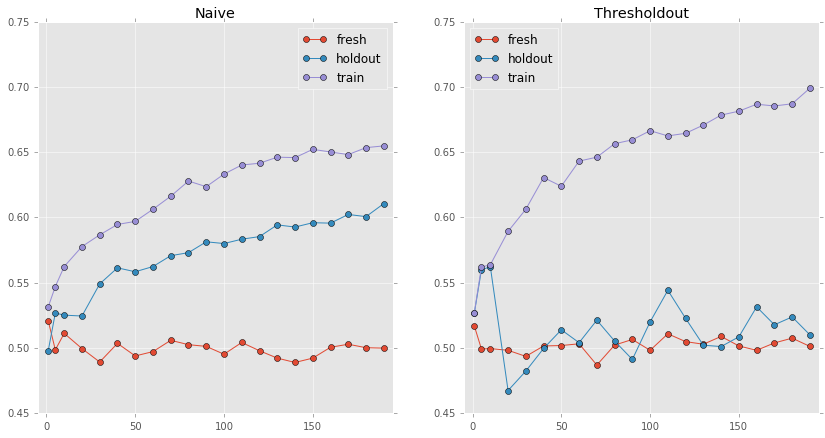
Here we see the accuracy of our classifier as a function of the number of features we selected for both methods. This experiment can be used to tune the hyper-parameter that control the number of selected features. In the left plot, we can clearly see the naive method overfits to the holdout set.  The holdout accuracy follows the trend of the training accuracy, which increases as we select more variables. However, the fresh accuracy stays constant at 50%, which means that the accuracy computed over the holdout set is contaminated and cannot be used for model selection, or to estimate the generalization error.

The right plot shows a completely different story. The holdout accuracy doesn’t follow the training accuracy, it is much more similar to the fresh accuracy, which is exactly what we want! We can see that it mostly jumps around 50%, which is because Thresholdout guarantees that the expected accuracy will be similar to the fresh accuracy (within certain limits).

In the next figure, I repeated the experiment only with 10 informative features, and again you can see very similar results. Using the Naive method, the holdout accuracy follows the trend of the training accuracy, but when using Thresholdout it follows the fresh accuracy.

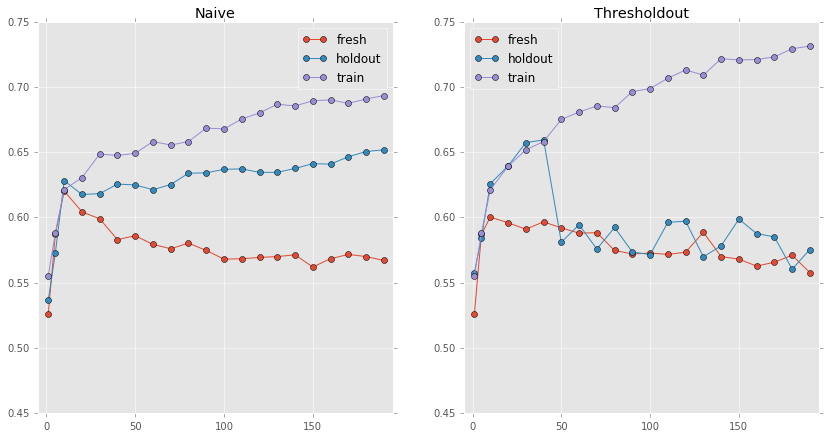
So what’s happening here? Let’s break down the algorithm to get the intuition behind it. Every time we need to compute a statistic over the holdout set, we have to go through the Thresholdout function. In this example it happens twice: We first compute the correlation coefficient in the feature selection step, and then the accuracy when we evaluate the classifier. Thresholdout compares the statistic to the one computed over the training set, and if the difference is smaller than $\tau$, it returns the training statistic. The intuition here is that if the two statistics are close, then our model/choice/query generalizes to the holdout set, so there is no need to expose the holdout statistic, it’s enough to return the training statistic because it’s close enough. Remember, we don’t want to expose our holdout static, so the algorithm won’t overfit to the holdout set.

But what happens when our training statistic is far from the holdout statistic? In this case, we are going to return the holdout static with some added noise. The idea here is that we need to tell to the analyst that the model is off and by how much, but we do add small noise to it to not leak information about the holdout set.

So the algorithm never exposes the holdout statistic itself. What the analyst sees is a statistic that is close to what she is looking for: a holdout static with noise, or the training statistic when the two are very similar.

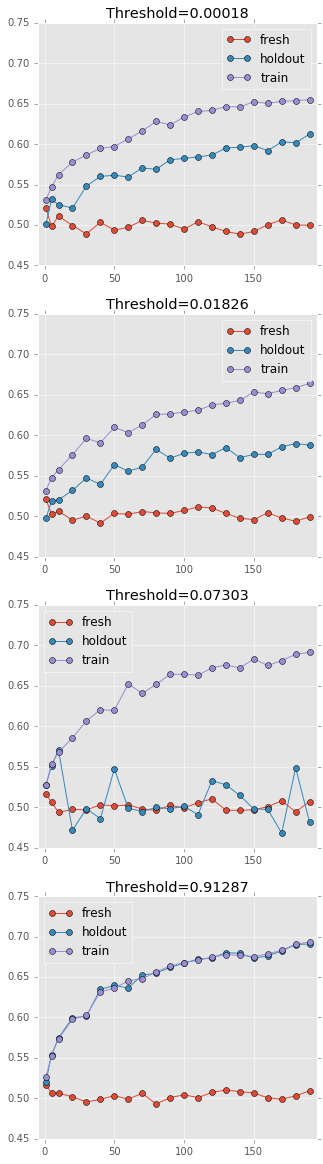
If you look again at the figure above, you can notice that Thresholdout’s largest overestimates are when we select a small number of features (10-40). The reason for this is that when we select a small set of features the difference between the training accuracy and the holdout accuracy is smaller than the threshold so it returns the training statistic. It’s the price we need to pay to retain an uncontaminated holdout set.

Note that using cross-validation in this scenario will not solve our problem. Since in every iteration of the procedure we will double dip and therefore overestimate our accuracy.

For Thresholdout to work there are two parameters that we need to set: The threshold ($\tau$), and the noise term. According to Dwork et al, we can simply set the standard deviation of the noise to be smaller than  $\tau$ by a small factor, like 4. So now we are left with the problem of setting up $\tau$. As we mentioned, if the difference between M(S_t) and M(S_h) is smaller than $\tau$ we consider them to be close, which means that $\tau$ represents the acceptable noise level we expect when computing the same static on the holdout set. For instance, we expect the average difference to decrease as the size of holdout set increases, as small datasets tend to produce more extreme statistics.

Overall setting this parameter can be tricky, if we set it to be too small, we are saying that we don’t tolerate even a small difference between M(S_t) and M(S_h). Thresholdout will then return the noisy holdout stat many more times than necessary, and we will start fitting to the holdout set. If we set it to high, we’re saying that we tolerate even larger differences between the statistics. The algorithm will then return the training statistic too often, which effectively translates to completely ignoring the holdout set, and just fitting to the training set.

Here is a simulation of how it looks in practice:

There are several implications to this work:

• Adaptive analysis and valid exploratory analysis: Many false findings in exploratory analysis are due to the garden of forking path problem, where researchers make multiple comparisons without being able to control for them. Thresholdout provides a framework which protects researchers from this problem.
• Automatic Machine learning: Today there are many packages that allow us to compare many types of algorithms, feature transformation, and parameters set with a touch of a button. To speed up this process, we need a much smarter way to test all of these options. Thresholdout provides a mechanism to perform a valid sequential testing of these models on the same holdout set.
• Simplify training with Structured data.  Let’s say our data has a time component to it. For instance, in Zillow’s recommendation services, we’re trying to predict which listings our users will want to see tomorrow based on their viewing history. We can take the data from day 1 to t for training, day t+1 for validation, and day t+2 for testing. But then we have a problem, if we train our model using the first t days, we cannot test it on day t+2, since it is supposed to predict one day ahead and not two. So we can validate it on t+1, and then retrain on the first t+1 days, but this is very time consuming, and it also means we train on our validation set. Alternatively, with Thresholdout we can use the validation set as a test set.
• Determining leaderboard leader in machine learning competitions: As we mention in the beginning, the leaderboard in machine learning competitions cause teams to overfit. A recently published work based on the Thresholdout mechanism shows how we can solve this problem.

Of course, Thresholdout comes with drawbacks. The first, as we mentioned before, is setting up the threshold, which is not trivial. The second is that the method performs worse than simply using multiple holdout sets. But then again it tries to solve the problem that we do not know in advance how many holdout sets we need, and sometimes it’s just costly to create them.

To summarize, Thresholdout and similar work based on differential privacy allow us to use a single holdout set for all of our validation needs, and by doing so speeding up the modeling process while maintaining statistical validity of the results. I hope that soon we will see Thresholdout algorithm incorporated into more standard data science libraries so it will become mainstream.